技术原理

引言

在超声波气体流量和速度测量中，了解测量方法的技术原理对于正确选择和应用测量系统至关重要。本章将深入探讨时差法、互相关法和多普勒法三种主要的超声波测量方法的技术原理，包括数学推导、工作机制、优缺点和适用场景。

超声波基础回顾

在详细讨论各个测量方法之前，回顾一下超声波在气体介质中的传播特性非常重要。

• 声速 c ：取决于气体的温度、压力和成分，通常由以下公式计算：

    其中：

             • λ：气体的比热容比（定压比热容与定容比热容之比）

             • R：气体常数

             • T：绝对温度

• 衰减：超声波在气体中传播时，能量会逐渐衰减，衰减系数与频率的平方成正比。

• 反射和折射：当超声波遇到不同介质的界面时，会发生反射和折射，影响声波的传播路径和强度。

时差法（Time-of-Flight，TOF）

原理概述

时差法是超声波流量计最常用的方法，基于超声波在顺流和逆流方向上的传播时间差来计算流体的平均流速。

工作机制

1. 传感器布置：在管道的上下游安装一对超声波换能器，通常以一定角度对称安装。

2. 信号传输：

  • 顺流方向：超声波从上游换能器（A）发射，沿着流体流动方向传播到下游换能器（B）。

  • 逆流方向：超声波从下游换能器（B）发射，逆着流体流动方向传播到上游换能器（A）。

3. 时间测量：

  • 测量超声波在顺流和逆流方向上的传播时间，分别记为t_down和 t_up。

4. 流速计算：

  • 根据两次传播时间的差异，计算流体的平均流速 v 。

数学推导

1. 传播时间表达式

• 顺流方向传播时间：

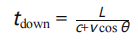
• 逆流方向传播时间：

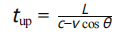
其中：

• L ：换能器之间的声程距离

• c：介质中的声速

• v：流体的平均流速

• θ：声波传播方向与管道轴线之间的夹角

2. 时间差计算

    计算传播时间差 △t：

3. 流速表达式

    通过整理上式，得到流速 v的表达式：

    由于声速 c 可能未知或变化，可以通过测量 t_down和 t_up的乘积或平均值来消除 c 的影响。

4. 实际计算公式

在实际应用中，常用以下近似公式计算流速：

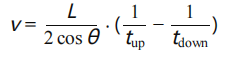
或者：

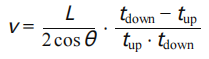
 优点

• 高精度：能够实现高精度的流量测量，误差通常在±1%以内。

• 无活动部件：无机械磨损，维护量小。

• 适用范围广：可用于各种管径和流体类型。

 缺点

• 对时间测量精度要求高：需要纳秒级的时间测量精度。

• 安装要求严格：换能器的安装角度和位置需要精确，管道内流场应稳定。

 适用场景

• 洁净流体：适用于清洁、均匀的流体。

• 工业管道：广泛用于水、气体、石油等管道的流量测量。

互相关法

原理概述

互相关法利用随机扰动信号在流体中的传输特性，通过计算上下游传感器接收信号的互相关函数，确定流体的流速。

工作机制

1. 扰动信号产生：

• 流体中的自然扰动（如湍流）或人为引入的扰动（如随机噪声）。

2. 传感器布置：

• 在上下游位置安装两个传感器，距离为 D。

3. 信号采集：

• 同时采集上下游传感器接收到的信号，记为 x(t)  和  y(t)。

4. 互相关函数计算：

• 计算上下游信号的互相关函数 Rxy（τ）。

5. 时间延迟确定：

• 互相关函数在时间延迟τ=△t处达到最大值，表示扰动信号从上游传输到下游的时间差。

6. 流速计算：

数学原理

1. 互相关函数定义

互相关函数 Rxy（τ）定义为：

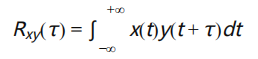
• 当τ=△t时，互相关函数达到最大值。

2. 流速计算

• 由于扰动信号以流速 v 传输，从上游到下游的时间差为：

• 通过测量 △t，可以计算流速  v 。

优点

• 对流场分布不敏感：适用于湍流和不稳定流动。

• 抗干扰能力强：对外界噪声和干扰具有较好的抑制能力。

缺点

• 计算量大：需要大量数据处理和计算资源。

• 实时性受限：不适合要求高实时性的应用。

适用场景

• 湍流流体：如气体、蒸汽等。

• 大型管道：管径较大，流场复杂的情况下。

多普勒法

原理概述

多普勒法基于多普勒效应，通过测量超声波频率的偏移来计算流体的速度，适用于含有散射体（如微粒、气泡）的流体。

多普勒效应简介

• 多普勒效应：当波源和接收器之间存在相对运动时，接收到的波的频率会发生变化。

• 频率偏移 △f：与相对速度  v 成正比。

工作机制

1. 超声波发射：

• 换能器以已知频率 f₀ 发射超声波进入流体。

2. 散射体反射：

• 超声波遇到流体中的散射体，被反射回换能器。

3. 信号接收：

• 换能器接收反射回来的超声波，频率发生偏移f 。

4. 频率偏移测量：

• 计算接收信号的频率偏移 f = f - f₀ 。

5. 流速计算：

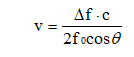
   其中：

• c：介质中的声速

• θ：超声波入射角度

数学推导

•  发射波的频率：f₀

•  散射体运动导致的频率偏移：

            • 第一次多普勒偏移（发射到散射体）：

           • 第二次多普勒偏移（散射体到接收器）：

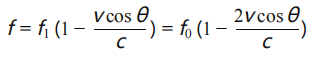
• 频率偏移：

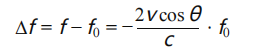
• 流速计算：

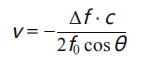
  由于测量的是频率偏移的绝对值，流速 v 为正值。

优点

• 可测量局部流速：适用于测量流体内部的速度分布。

• 对流动方向敏感：能够区分流动的方向。

缺点

• 需要散射体：流体中必须存在足够的反射颗粒。

• 信号处理复杂：需要高精度的频率测量和信号处理。

适用场景

• 含颗粒或气泡的流体：如污水、含尘气体等。

• 需要测量速度分布的场合：如研究流体力学特性。

方法比较与选择

方法比较

选择原则

• 根据流体特性：

       • 洁净流体：优先选择时差法。

       • 湍流或含有扰动的流体：互相关法效果较好。

       • 含有散射体的流体：多普勒法是唯一选择。

• 根据测量需求：

      • 高精度、实时性：时差法。

      • 研究流体特性、速度分布：多普勒法。

      • 根据应用条件：

      • 安装空间有限、安装困难：需要考虑传感器布置的灵活性。

总结

本章深入探讨了时差法、互相关法和多普勒法三种超声波气体测量方法的技术原理。通过对各自的工作机制、数学推导、优缺点和适用场景的详细分析，可以帮助用户根据实际需求选择最合适的测量方法。

理解这些技术原理对于设计和优化超声波测量系统至关重要。正确的测量方法选择和系统设计，将显著提高测量的精度、可靠性和适用性，为工业过程控制和流体力学研究提供强有力的支持。